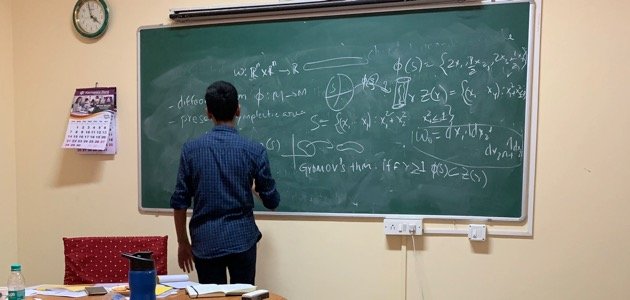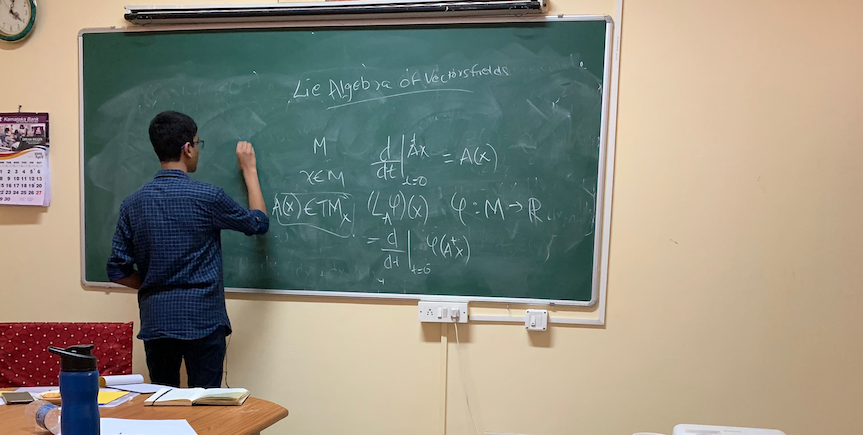It is 3 pm at the Poornaprajna Institute of Scientific Research (PPISR), Bangalore, India. The faculty and research students have gathered at the auditorium to attend a seminar entitled, “Symplectic Geometry, Geometric Mechanics and Lagrangian Manifolds.” It is obvious to everyone that the talk is of a very advanced level and possible only by someone who has completed a Ph. D or a mature researcher in the field. But what is absolutely surprising to all is the fact that the speaker is formally an eighth grade student!
The student walks in. Everyone looks to the Power-Point presentation that they expect he would be using. But the bright young student has none. Instead, he declares that he would be working on the whiteboard. He has only an outline of his presentation in his notes. The seminar begins. The speaker soon fills the whiteboard with equations writing rapidly as he speaks. In just a few minutes he has completely expounded the elements of Symplectic Geometry and goes on to present the finer aspects of Geometric Mechanics.
He explains with great lucidity the meaning of symplectomorphisms, the role of the Stiefel-Whitney characteristic class, symplectic rigidity, symplectic capacities, and the Gromov non-squeezing theorem leading to the symplectic camel theorem. The rapidity of his speech is equally astounding and the flow flawless. He encourages interaction and pauses between to address queries, clarifies points and continues to bring out the significance of the geometric and topological formulation of Hamiltonian mechanics. A the end of the seminar, the audience is spellbound. They wonder at what they have beheld. Is it really true that this student is only in his eighth grade? How could he master such advanced topics at so young an age?

The student, Kartik (name changed to protect identity from general publicity) is in his eighth grade at school but what is more significant, he is also a research student of the Advanced Learner’s program at the Centre for Fundamental Research and Creative Education (CFRCE), Bangalore, India. Having enrolled for the program in the beginning of his eight grade, he has in less than a year’s time, completely mastered a substantial portion of Theoretical Physics including Classical Mechanics, Classical Electrodynamics, Classical Theory of Fields, General Relativity, Differential Geometry and Topology, Symplectic Geometry, Geometric Mechanics and Geometric Quantization.
Gromov’s Non–Squeezing theorem leads to the Symplectic Camel theorem
At an age when students are just beginning to become aware of the division of science into physics, chemistry and biology, several students at CFRCE are already deep into research studies in diverse domains especially theoretical physics, mathematics, astronomy and astrophysics, computer science, artificial intelligence and machine learning, robotics etc. Kartik himself is one of the most advanced of such students. How has this come to be? Are all these students prodigies exceptionally gifted with intellectual capacity? Or is there a very special method that CFRCE has developed that makes this possible? Several are the questions that occur to an inquiring person and will be addressed in a book that deals especially with the unique philosophy and methodology of CFRCE.

Kartik began his studies at CFRCE just as he was entering his eighth grade. He was one of a very select group of students who made it to the CFRCE Advanced Learner’s program. The selection criterion to this program is rigorous and completely different from most conventional institutions. For, at CFRCE, formal academic achievements or grades occupy only a minor role. What really matters is the student’s sense of purpose, interest and passion and a strong self-drive. In addition the student needs to have already taken some kind of initiative to learn independently ahead of school.

Kartik’s interest in science began at an early age. He was particularly intrigued by the vast order and regularity to be found in Nature. Even more so was the fact that this order could be grasped by mathematical thinking. This motivated him to look for books that were a little more technical than most popular books. He soon came across two fine books that did address his quest, one was Stephen Hawking’s, “A Brief History of Time,” and the other a much more involved and demanding book, Kip Thorne’s, “Black Holes and Time Warps.” Reading these gave Kartik a glimpse not only of what theoretical physics was all about but also of the great personalities behind the magnificent edifice of natural philosophy. Now was the time to go more technical. He looked up resources on the internet like the Khan Academy videos and websites of eminent physicists and mathematicians. After dipping into these he was filled with a sense of deep commitment and dedication to the domain of theoretical physics. He realized that theoretical physics was his calling. Through this field he could explore Nature through mathematical thinking and expand the boundaries of human knowledge. For this he needed a more systematic guidance and support.
Kartik had an additional privilege and advantage. His cousin Shreya had been a CFRCE student for two years starting from her 9th grade and had already mastered a similar range of topics in theoretical physics and was deep into research on Black Hole Physics. Shreya had informally guided Kartik and initiated him into advanced studies. Thus it was that Kartik was more prepared than most other students who were entering the program. After a brief meeting with the program director, it was recommended that Kartik be sent the application form. After receiving it, Kartik completed it along with the mandatory statement of purpose (SOP) that every student aspiring to enter the program is required to. Sure enough, Kartik was selected and enrolled in the program. Thus began his serious learning in theoretical physics. Guided by his mentors, he completed the elements of Precalculus like Algebra, Trigonometry and Coordinate Geometry and Newtonian Mechanics in around a month’s time paralleling it with his reading of Roger Penrose’s, “Road to Reality.” In around two month’s time he completed Calculus and was ready to take on his dream, theoretical physics. He began with Landau and Lifshitz’s Course of Theoretical Physics, Vol 1, Mechanics.
As this was his first real encounter with serious theoretical physics, he was enthralled by the beauty fo the subject and went through it with great eagerness. The Lagrangian formulation of mechanics motivated him to explore the Calculus of Variations from other sources also to supplement his studies. He was struck by the meaning of the necessary and sufficient conditions for an extremal of a variational problem. As he was looking a little more deeply at the sufficient conditions, he realised that it would soon lead him to General Relativity via the Jacobi geodesic deviation equation. In around a month’s time, Kartik had completed the first Volume. He now took on the second Volume, “The Classical Theory of Fields.” However, he had been so captivated by the meaning of Classical Mechanics that he wanted to explore it in more detail. V I Arnold’s, “Mathematical Methods of Classical Mechanics,” was the book that attracted him at this stage and he plunged into it. And as he was already interested in geodesics and geodesic deviation, he started studying Misner, Thorne and Wheeler’s, “Gravitation,” alongside.
In addition to this mainstream pursuits, he was also building up his learning in Electrodynamics, Mathematical Methods, and especially Black Hole Physics via the book by Novikov and Frolov’s, “The Physics of Black Holes.” In around nine month’s time since his program began, Kartik had mastered modern Differential Geometry and Topology including Differential Forms, Manifolds, Vector Bundles, Principal Fiber Bundles, Connections and Curvature, Cartan Structure Equations, Cohomology, Lie groups and Lie Algebras and of course, most of Symplectic Geometry and Geometric Mechanics. He presented the fruits of his learning in three talks at CFRCE. He had just entered into his pursuit of Gromov’s non-squeezing theorem and Lagrangian Manifolds when he received the invitation to give a talk at the Poornaprajna Institute of Scientific Research (PPISR). As Kartik was entering his second year at CFRCE, and his ninth grade at school, he was already deep into his inquiries on symplectic rigidity and symplectic capacities and Geometric Quantization.
The main lesson to take from the above experience is this: conventional educational systems have grossly and subtly underestimated the capabilities of children. Despite several thinkers on education pointing out the tremendous potential of thew child mind and despite advances in cognitive neuroscience and cognitive psychology and a host of other disciplines like multiple intelligences, performance psychology, standard educational practice still considers the child mind more like a tabula rasa, a blank slate into which the wisdom of teachers is supposed to be poured into in the form of lectures in classrooms. On the contrary, when children are taken to be what they really are, human beings in a transitional state of tremendous intelligence and high brain processing speeds, the results obtained are found to be nothing short of miraculous.
For nearly two decades CFRCE education has been doing precisely this: empowering children to take complete charge of their learning and engaging themselves in learning at the graduate and doctoral levels. Though profound, more so is the recognition of the profundity of the neuro-cognitive potential in the children that is the true hallmark of CFRCE education. The recent book by Dr. B S Ramachandra, – Leonardo and Da Vinci- The Tao of Meta-Learning draws upon the extensive case studies and notes kept by the mentors on actual interactions with students and insights gained in the process of leading them along what is now known at CFRCE as super fast accelerated learning. The purpose is to demonstrate how the deepest potential of students may be actualised by giving careful attention to the neuro-cognitive potential.